javascript-algorithms

Estrutura de Dados e Algoritmos em JavaScript

Este repositório contém exemplos baseados em JavaScript de muitos algoritmos e estruturas de dados populares.

Cada algoritmo e estrutura de dado possui seu próprio README com explicações relacionadas e links para leitura adicional (incluindo vídeos para YouTube)

Leia isto em outros idiomas: English 简体中文, 繁體中文, 한국어, 日本語, Polski, Français, Español

Data Structures

Uma estrutura de dados é uma maneira particular de organizar e armazenar dados em um computador para que ele possa ser acessado e modificado de forma eficiente. Mais precisamente, uma estrutura de dados é uma coleção de dados valores, as relações entre eles e as funções ou operações que podem ser aplicadas a os dados.

B - Iniciante, A - Avançado

• B Lista Encadeada (Linked List)
• B Lista Duplamente Ligada (Doubly Linked List)
• B Fila (Queue)
• B Stack
• B Tabela de Hash (Hash Table)
• B Heap
• B Fila de Prioridade (Priority Queue)
• A Árvore de prefixos (Trie)
• A Árvore (Tree)
  • A Árvore de Pesquisa Binária (Binary Search Tree)
  • A Árvore AVL (AVL Tree)
  • A Árvore Vermelha-Preta (Red-Black Tree)
  • A Árvore de Segmento (Segment Tree) - com exemplos de consultas min / max / sum range
  • A Árvore Fenwick (Fenwick Tree) (Árvore indexada binária)
• A Gráfico (Graph) (ambos dirigidos e não direcionados)
• A Conjunto Disjuntor (Disjoint Set)
• A Filtro Bloom (Bloom Filter)

Algoritmos

Um algoritmo é uma especificação inequívoca de como resolver uma classe de problemas. Isto é um conjunto de regras que define precisamente uma sequência de operações.

B - Iniciante, A - Avançado

Algoritmos por Tópico

• Matemática
  • B Manipulação Bit - set/get/update/clear bits, multiplicação / divisão por dois, tornar negativo etc.
  • B Fatorial
  • B Número de Fibonacci
  • B Teste de Primalidade (método de divisão experimental)
  • B Algoritmo Euclidiano - calcular o maior divisor comum (GCD)
  • B Mínimo múltiplo comum (LCM)
  • B Peneira de Eratóstenes - encontrar todos os números primos até um determinado limite
  • B Potência de dois - verifique se o número é a potência de dois (algoritmos ingênuos e bit a bit)
  • B Triângulo de Pascal
  • B Número complexo - números complexos e operações básicas com eles
  • A Partição inteira
  • A Algoritmo Liu Hui π - cálculos aproximados de π baseados em N-gons
• Conjuntos
  • B Produto cartesiano - produto de vários conjuntos
  • B Permutações de Fisher–Yates - permutação aleatória de uma sequência finita
  • A Potência e Conjunto - todos os subconjuntos de um conjunto
  • A Permutações (com e sem repetições)
  • A Combinações (com e sem repetições)
  • A Mais longa subsequência comum (LCS)
  • A Maior subsequência crescente
  • A Supersequência Comum mais curta (SCS)
  • A Problema da mochila - “0/1” e “Não consolidado”
  • A Máximo Subarray - “Força bruta” e “ Programação Dinâmica” versões (Kadane’s)
  • A Soma de Combinação - encontre todas as combinações que formam uma soma específica
• Cadeia de Caracteres
  • B Hamming Distance - número de posições em que os símbolos são diferentes
  • A Levenshtein Distance - distância mínima de edição entre duas sequências
  • A Knuth–Morris–Pratt Algorithm (Algoritmo KMP) - pesquisa de substring (correspondência de padrão)
  • A Z Algorithm - pesquisa de substring (correspondência de padrão)
  • A Rabin Karp Algorithm - pesquisa de substring
  • A Longest Common Substring
  • A Regular Expression Matching
• Buscas
  • B Linear Search
  • B Jump Search (ou Bloquear pesquisa) - pesquisar na matriz ordenada
  • B Binary Search - pesquisar na matriz ordenada
  • B Interpolation Search - pesquisar em matriz classificada uniformemente distribuída
• Classificação
  • B Bubble Sort
  • B Selection Sort
  • B Insertion Sort
  • B Heap Sort
  • B Merge Sort
  • B Quicksort - implementações local e não local
  • B Shellsort
  • B Counting Sort
  • B Radix Sort
• Arvóres
  • B Depth-First Search (DFS)
  • B Breadth-First Search (BFS)
• Gráficos
  • B Depth-First Search (DFS)
  • B Breadth-First Search (BFS)
  • B Kruskal’s Algorithm - encontrando Árvore Mínima de Abrangência (MST) para grafo não direcionado ponderado
  • A Dijkstra Algorithm - encontrar caminhos mais curtos para todos os vértices do grafo a partir de um único vértice
  • A Bellman-Ford Algorithm - encontrar caminhos mais curtos para todos os vértices do grafo a partir de um único vértice
  • A Floyd-Warshall Algorithm - encontrar caminhos mais curtos entre todos os pares de vértices
  • A Detect Cycle - para gráficos direcionados e não direcionados (versões baseadas em DFS e Conjunto Disjuntivo)
  • A Prim’s Algorithm - encontrando Árvore Mínima de Abrangência (MST) para grafo não direcionado ponderado
  • A Topological Sorting - Métodos DFS
  • A Articulation Points -O algoritmo de Tarjan (baseado em DFS)
  • A Bridges - Algoritmo baseado em DFS
  • A Eulerian Path and Eulerian Circuit - Algoritmo de Fleury - Visite todas as bordas exatamente uma vez
  • A Hamiltonian Cycle - Visite todas as bordas exatamente uma vez
  • A Strongly Connected Components - Algoritmo de Kosaraju’s
  • A Travelling Salesman Problem - rota mais curta possível que visita cada cidade e retorna à cidade de origem
• criptografia
  • B Polynomial Hash - função de hash de rolagem baseada em polinômio
• Sem categoria
  • B Tower of Hanoi
  • B Square Matrix Rotation - algoritmo no local
  • B Jump Game - backtracking, programação dinâmica (top-down + bottom-up) e exemplos gananciosos
  • B Unique Paths - backtracking, programação dinâmica e exemplos baseados no triângulo de Pascal
  • B Rain Terraces - trapping problema da água da chuva (programação dinâmica e versões de força bruta)
  • A N-Queens Problem
  • A Knight’s Tour

Algoritmos por Paradigma

Um paradigma algorítmico é um método ou abordagem genérica subjacente ao design de uma classe de algoritmos. É uma abstração maior do que a noção de um algoritmo, assim como algoritmo é uma abstração maior que um programa de computador.

• Força bruta - look at all the possibilities and selects the best solution
  • B Linear Search
  • B Rain Terraces - trapping problema da água da chuva
  • A Maximum Subarray
  • A Travelling Salesman Problem - rota mais curta possível que visita cada cidade e retorna à cidade de origem
• Greedy - choose the best option at the current time, without any consideration for the future
  • B Jump Game
  • A Unbound Knapsack Problem
  • A Dijkstra Algorithm - finding shortest path to all graph vertices
  • A Prim’s Algorithm - encontrando Árvore Mínima de Abrangência (MST) para grafo não direcionado ponderado
  • A Kruskal’s Algorithm - encontrando Árvore Mínima de Abrangência (MST) para grafo não direcionado ponderado
• Divide and Conquer - dividir o problema em partes menores e depois resolver essas partes
  • B Binary Search
  • B Tower of Hanoi
  • B Pascal’s Triangle
  • B Euclidean Algorithm - calculate the Greatest Common Divisor (GCD)
  • B Merge Sort
  • B Quicksort
  • B Tree Depth-First Search (DFS)
  • B Graph Depth-First Search (DFS)
  • B Jump Game
  • A Permutations (com e sem repetições)
  • A Combinations (com e sem repetições)
• Dynamic Programming - criar uma solução usando sub-soluções encontradas anteriormente
  • B Fibonacci Number
  • B Jump Game
  • B Unique Paths
  • B Rain Terraces - trapping problema da água da chuva
  • A Levenshtein Distance - distância mínima de edição entre duas sequências
  • A Longest Common Subsequence (LCS)
  • A Longest Common Substring
  • A Longest Increasing Subsequence
  • A Shortest Common Supersequence
  • A 0/1 Knapsack Problem
  • A Integer Partition
  • A Maximum Subarray
  • A Bellman-Ford Algorithm - encontrando o caminho mais curto para todos os vértices do gráfico
  • A Floyd-Warshall Algorithm - encontrar caminhos mais curtos entre todos os pares de vértices
  • A Regular Expression Matching
• Backtracking - da mesma forma que a força bruta, tente gerar todas as soluções possíveis, mas cada vez que você gerar a próxima solução, você testará se satisfizer todas as condições, e só então continuar gerando soluções subseqüentes. Caso contrário, volte atrás e siga um caminho diferente para encontrar uma solução. Normalmente, a passagem DFS do espaço de estados está sendo usada.
  • B Jump Game
  • B Unique Paths
  • A Hamiltonian Cycle - Visite todos os vértices exatamente uma vez
  • A N-Queens Problem
  • A Knight’s Tour
  • A Combination Sum - encontre todas as combinações que formam uma soma específica
• Branch & Bound - lembre-se da solução de menor custo encontrada em cada etapa do retrocesso pesquisar e usar o custo da solução de menor custo encontrada até o limite inferior do custo de solução de menor custo para o problema, a fim de descartar soluções parciais com custos maiores que o solução de menor custo encontrada até o momento. Normalmente, a travessia BFS em combinação com a passagem DFS do espaço de estados árvore está sendo usada

Como usar este repositório

Instalar todas as dependências

npm install

Executar o ESLint

Você pode querer executá-lo para verificar a qualidade do código.

npm run lint

Execute todos os testes

npm test

Executar testes por nome

npm test -- 'LinkedList'

Parque infantil

Você pode brincar com estruturas de dados e algoritmos em ./src/playground/playground.js arquivar e escrever testes para isso em ./src/playground/__test__/playground.test.js.

Em seguida, basta executar o seguinte comando para testar se o código do seu playground funciona conforme o esperado:

npm test -- 'playground'

Informação útil

Referências

▶ Estruturas de dados e algoritmos no YouTube

Notação Big O

Ordem de crescimento dos algoritmos especificados em notação Big O.

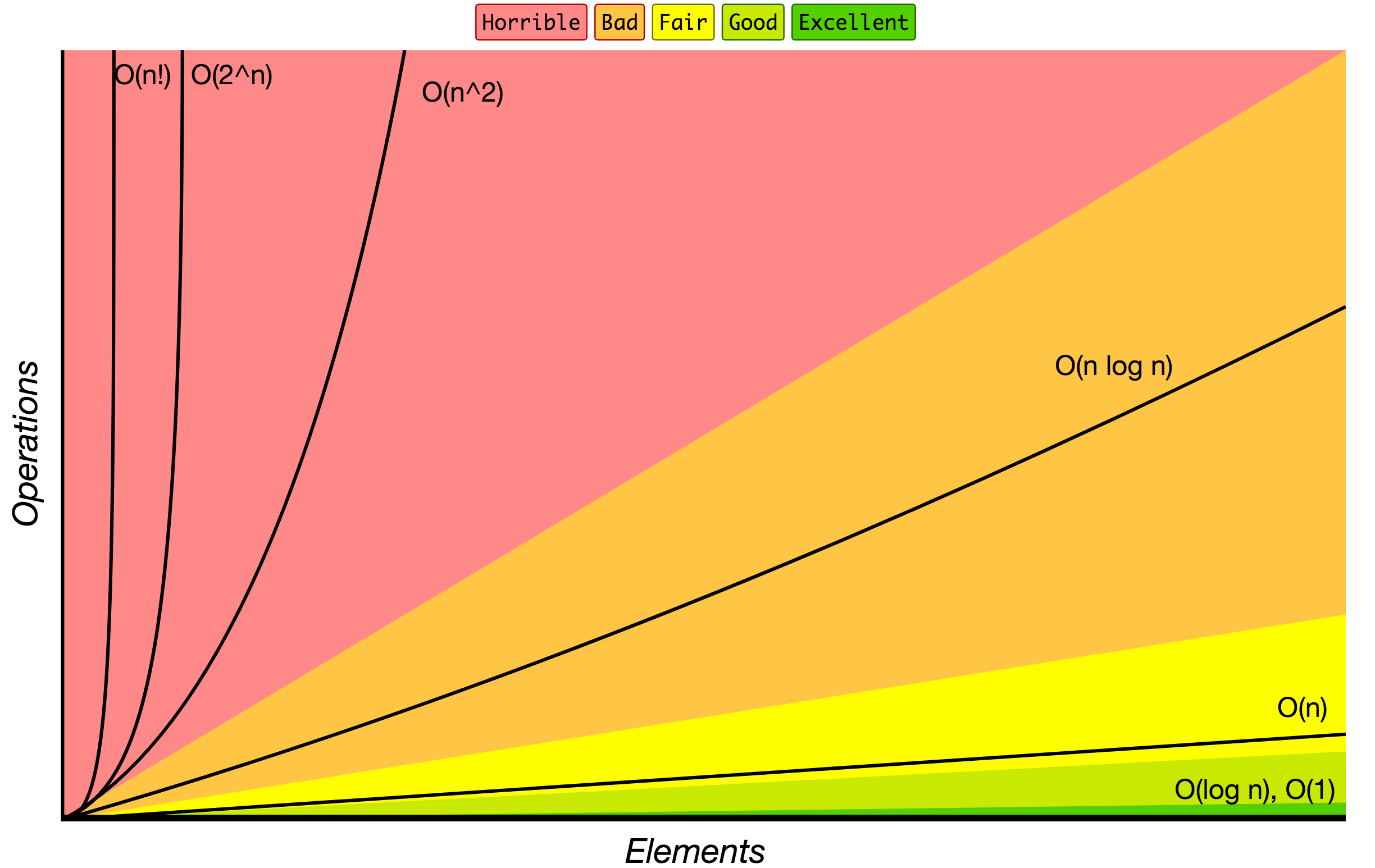
Fonte: Notação Big-O dicas.

Abaixo está a lista de algumas das notações Big O mais usadas e suas comparações de desempenho em relação aos diferentes tamanhos dos dados de entrada.

Notação Big-O	Cálculos para 10 elementos	Cálculos para 100 elementos	Cálculos para 1000 elementos
O(1)	1	1	1
O(log N)	3	6	9
O(N)	10	100	1000
O(N log N)	30	600	9000
O(N^2)	100	10000	1000000
O(2^N)	1024	1.26e+29	1.07e+301
O(N!)	3628800	9.3e+157	4.02e+2567

Complexidade de operações de estrutura de dados

estrutura de dados	Acesso	Busca	Inserção	Eliminação	comentários
Array	1	n	n	n
Stack	n	n	1	1
Queue	n	n	1	1
Linked List	n	n	1	1
Hash Table	-	n	n	n	Em caso de uma função hash perfeita, os custos seriam O (1)
Binary Search Tree	n	n	n	n	No caso de custos de árvore equilibrados seria O (log (n))
B-Tree	log(n)	log(n)	log(n)	log(n)
Red-Black Tree	log(n)	log(n)	log(n)	log(n)
AVL Tree	log(n)	log(n)	log(n)	log(n)
Bloom Filter	-	1	1	-	Falsos positivos são possíveis durante a pesquisa

Array Sorting Algorithms Complexity

Nome	Melhor	Média	Pior	Mémoria	Estável	comentários
Bubble sort	n	n2	n2	1	Sim
Insertion sort	n	n2	n2	1	Sim
Selection sort	n2	n2	n2	1	Não
Heap sort	n log(n)	n log(n)	n log(n)	1	Não
Merge sort	n log(n)	n log(n)	n log(n)	n	Sim
Quick sort	n log(n)	n log(n)	n2	log(n)	Não	O Quicksort geralmente é feito no local com o espaço de pilha O O(log(n)) stack space
Shell sort	n log(n)	depende da sequência de lacunas	n (log(n))2	1	Não
Counting sort	n + r	n + r	n + r	n + r	Sim	r - maior número na matriz
Radix sort	n * k	n * k	n * k	n + k	Sim	k - comprimento da chave mais longa

This site is open source. Improve this page.